
” It does not depend on what particular sequence of numbers is chosen to represent x it is only necessary that the sequence converge to a limit. This is written formally as:Īnd reads “The limit of f of x, as x approaches p, equals L. More generally when the value of a function f (x) approaches a definite value L as the independent variable x gets close to a real number p then L is called the limit of the function. If this sequence is a converging sequence then the limit of that sequence is called the limit of the function. In fact, whenever the values of x form a sequence, the values f (x) also form a sequence. The question arises as to what the values of the function do, that is, what happens to successive values of y. When the elements of the ordered pairs are real numbers, the relationship is usually expressed in the form of an equation.) Suppose that successive values of x are chosen to match those of a converging sequence such as the sequence S from the previous example. (A function is a set of ordered pairs for which the first and second elements of each pair are related to one another in a fixed way. Limit of a functionĬonsider an arbitrary function, y = f (x). If an infinite sequence diverges, the running total of the terms eventually turns away from any specific value, so a divergent sequence has no limiting sum. The numbers in the sequence never quite reach the limit, but they never go past it either. For this sequence (1/2) n gets arbitrarily close to 0, so 0 is the limit of the sequence. The sequence is said to converge, meaning numbers that are very far along in the sequence (corresponding to large “N ”) get very close together and very close to a single value called the limit.Ī sequence of numbers converges to a given number if the differences between the terms of the sequence and the given number form an infinitesimal sequence. Since (1/2) n equals 1/2 multiplied by itself n times, (1/2) n gets very small when n is allowed to become infinitely large. Thus, he argued, the distance (l) can never be fully traversed.Ĭonsider the sequence 1, 1/2, 1/4, 1/8.(1/2) n when n gets very large. Zeno argued that all motion was impossible because in order to move a distance (l) it is first necessary to travel half the distance, then half the remaining distance, then half of that remaining distance and so on. Limit of a sequenceĪncient Greek philosopher (of southern Italy) Zeno of Elea (c 490 –c 430 BC) may have been one of the first mathematicians to ponder the limit of a sequence and wonder how it related to the world around him.

English physicist and mathematician Sir Isaac Newton (1642 –1727) and German mathematician Gottfried Wilhelm Leibniz (1646 –1716) independently developed the general principles of calculus (of which the theory of limits is an important part) in the seventeenth century. Archimedes ’ thesis, The Method, was lost until 1906, when mathematicians discovered that Archimedes came close to discovering infinitesimal calculus.Īs Archimedes ’ work was unknown until the twentieth century, others developed the modern mathematical concept of limits. By carving these figures into small pieces that can be approximated, then increasing the number of pieces, the limit of the sum of pieces can give the desired quantity.

HistoryĪncient Greek mathematician Archimedes of Syracuse (287 –212 BC) first developed the idea of limits to measure curved figures and the volume of a sphere in the third century BC. Neighborhoods are definitive components of infinite limits of a sequence. Relevantly, a neighborhood of points near any given point comprise a neighborhood.

Nearness is key to understanding limits: only after nearness is defined does a limit acquire an exact meaning. Between any two real numbers there are always infinitely many more. The theory of limits is based on a particular property of the real numbers namely that between any two real numbers, no matter how close together they are, there is always another one. The operations of differentiation and integration from calculus are both based on the theory of limits. That is, a limit is a value that a variable quantity approaches as closely as one desires.
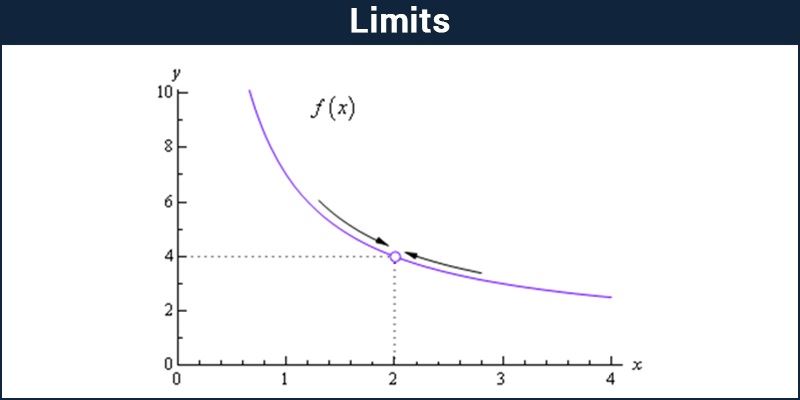
In mathematics the concept of limit formally expresses the notion of arbitrary closeness.


 0 kommentar(er)
0 kommentar(er)
